3.1 Solving Quadratic Equations Answers

We included H MH Into Math Course 8 Answer Key PDF Module 3 Lesson ane Solve Multi-stride Linear Equations to make students experts in learning maths.

HMH Into Math Course 8 Module 3 Lesson 1 Answer Key Solve Multi-step Linear Equations

I Can solve linear equations with integer and rational number coefficients.

Spark Your Learning
Jordan buys 2 new jerseys and a glove for softball. She pays the price shown for the glove and gives the clerk 2 l-dollar bills to pay the exact amount. How much does Jordan pay for each jersey? Write and solve an equation.

Reply:
The equation would be:
2x + 44 = 250
solving the equation:
2x = 250 – 44
2x = 206
10 = 206/2
x = 103.
Therefore, hashemite kingdom of jordan pays $103 for each jersey.
What would the equation and solution be if Jordan gives the clerk a single hundred-dollar bill? How are the equations alike or dissimilar? How is the process of solving the equations akin or different?

Answer:
If he gives $100 to the clerk and then the equation volition exist:
2x + 44 = 100
2x = 100 – 44
2x = 56
x = 56/two
ten = 28.

Turn and Talk Is there some other equation that will solve the same problem? Explain.

Build Understanding

one. A batting auto uses an automated baseball feeder. During baseball game practise the feeder is \(\frac{1}{6}\) total. An bellboy fills it with fifteen baseballs so that the feeder is at present \(\frac{ii}{3}\) full. How many baseballs does the feeder hold when full?
A. Write an equation to represent the trouble.


Respond:
The equation would exist:
1/6 x + 15 = ii/3 x
B. In lodge to isolate the variable, all terms containing x need to be on one side of the equation. How can y'all isolate the variable in the equation? What is the resulting equation before simplifying?
_____________________
_____________________
Answer:
ane/six x + 15 = two/3 10
Simplification:
subtract 15 from both sides
1/six x + 15 – fifteen = ii/3 ten – 15
1/six 10 = 2/3 x – 15
subtract 2/iii 10 from both sides
1/6 x – 2/iii x = 2/3 x – 15 – 2/3 x
take out mutual terms:
x(1/six – two/3) = -15
x(1-four/six) = -15
10(-3/6) = -15
X(-ane/ii) = -xv
-one/2 x = -15
C. Solve the equation for 10.
Answer:
by standing the respond from (B)
Multiply both sides by -2
(-one/2 x) (-two) = (-15)(-2)
x = 30
D. Await back at the original equation. How could you use the least mutual denominator of the fractions to rewrite the equation with integer coefficients? A coefficient is a number multiplied by the
variable.
________________________
Reply:
The original equation:
one/6 10 + xv = 2/3 ten
15 = ii/iii x – 1/6 x
15 = x(ii/iii – 1/6)
The LCM is 6
fifteen = 10(4 – i/6)
xv = x(5/6)
fifteen = v/6 ten
Eastward. What is the new equation? Solve this new equation. Practise you become the same solution?
________________________
Answer:
continuing from role (D)
The new equation is 15 = v/six x
switching the sides
multiply both sides past 6
(6) (5/6 10) = fifteen . vi
5x = 90
x = 18
No we didn't get the same solution.

This is an instance of a linear equation with only ane solution.

Turn and Talk Which equation did you prefer to work with? Why?

Pace It Out

2. Lanie and Jen buy the same number of books at the used book sale. Lanie buys paperback books and Jen buys hardcover books. Lanie spends $i.l less than Jen. Solve the equation to detect the number of books each of them buys.

1.2n – 1.5 = 0.45n
i.2n = 0.45n + ___
1.2n – ___ = ____
___ = ___
n = ____
Answer:
The given equation:
1.2n – 1.v = 0.45n
simplification:
1.2n = 0.45n + 1.5
1.2n – 0.45n = 1.5
0.8n = 1.5
n = ane.5/0.eight = 1.89
approximately 2.
Therefore, they buy 2 books each

A. Look at the decimals in the equation and remember near how you could rewrite the equation with integer coefficients. What is the to the lowest degree power of 10 you could multiply each term past to eliminate all the decimals?
___________________
Reply:
simplification:
Multiply both sides by 100
1.2n *100 – 1.five * 100 = 0.45n *100
120n – 150 = 45n
B. Multiply each term of the original equation to eliminate all the decimals. Solve the equation.
1.2n – 1.5 = 0.45n
___ (i.2n) — ___ (i.5) = ___ (0.45n)
___ northward – ___ = ___n
___n = ____
n = ____
Answer:
simplification:
Multiply both sides by 100
1.2n *100 – i.5 * 100 = 0.45n *100
120n – 150 = 45n
add 150 to both sides
120n – 150 + 150 = 45n + 150
120n = 45n + 150
120n – 45n = 150
75n = 150
n = 150/75
n = 2
C. Exercise you go the same solution?
___________________
Respond:
Yes, both are equal.
D. Which equation was easier to solve? Why?
___________________
Answer:
The equation that is non having decimals considering without decimals we can easily simplify the equation.

Turn and Talk How is solving an equation that involves fractions similar to solving an equation with decimals? What methods tin y'all use to solve each
Answer:
Simplify both sides of the equation by combining similar terms. If at that place are fractions, multiply both sides of the equation past the LCD (Least mutual denominator) of all the fractions. If in that location are decimals, multiply both sides of the equation by the lowest power of ten to convert them into whole numbers.

3. Jackie has a coupon for $8 off the cost of a jacket. Then the clerk takes 25% off the discounted price, and then she saves an additional $ten. Determine the original price of the jacket.
A. Write an equation using the Distributive Belongings, which states that for all real numbers a, b, and c, a(b + c) = ab + ac, and a(b – c) = ab – ac. Catechumen the percent to a fraction. Solve the equation.

\(\frac{one}{4}\)(p – 8) = 10

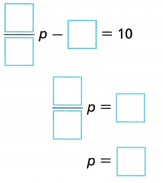
Answer:
The to a higher place-given equation:
i/4(p – eight) = 10
utilize distributive police force
i/4 p – 1/4 * 8 = 10
1/4p- 2 = ten
1/4 p = x + 2
ane/4 p = 12
multiply both sides by 4
4 * 1/4 p = 12 * 4
p = 48

B. Write the original equation, eliminate the fractions, and solve.
\(\frac{1}{4}\)(p – 8) = 10
four[\(\frac{ane}{4}\)(p – 8)] = 4(10)
p – ___ = ___
P = ___
Answer:
The above-given equation:
1/four(p – eight) = ten
to eliminate the factors, we need to multiply by iv both sides
(4) (i/4)[p- 8] = 10 * four
p – eight = 40
p = xl+ 8
p = 48

four. Solve the equation 4(two.5x + 2) – x = 26.9.
A. Apply the Distributive Property to write an equivalent equation.
__________________
Distributive law:
a(b + c) = ab + air conditioning
Answer:
The given equation:
4(2.5x + 2) – x = 26.9.
(4 * two.5x + iv * 2) – 10 = 26.9
10x + eight – x = 26.9
B. Combine like terms, terms that have the same variable raised to the aforementioned exponent, and solve.
__________________
Answer:
standing the part (A)
combine like terms:
9x + viii =26.ix
9x = 26.nine – eight
9x = 18.9
x = 18.ix/nine
10 = 2.1

Check Understanding

Question 1.
Anna spent $ii.75 at the school shop. She bought ii erasers and some pencils. How many pencils did she buy? Write and solve an equation.

Answer:
The cost of ii erasers = $0.25 10 2 = $0.5
The cost of pencils = P
The amount she spends in school store = $2.75
The equation:
0.5 + 0.75p = ii.75
0.75p = 2.75 – 0.v
p = ii.25/0.75
p = 3
Therefore, she buys three pencils.

Question 2.
Solve the equation. Check your solution. \(\frac{1}{5}\)(north – 10) = 6 – iii\(\frac{ane}{two}\)
Answer:
The given equation:
1/5(northward – 10) = 6 – 3 1/ii
catechumen mixed numbers to improper fractions
3 one/ii = 7/ii
1/v(n – x) = 6 – 7/2
1/5n – 1/v * 10 = 12 – 7/2
one/five n – 2 = five/two
1/five n = 5/2 + two
i/5 n = nine/two
multiply both sides by northward
v * 1/5 n = 5 * nine/2
n = 45/2
n = 22.5

On Your Own

Question three.
The sum of the measures of the angles in the triangle is 180°. What is the measure of each angle? Write and solve an equation.

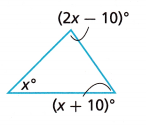
Answer:
(2x – 10) + (x + 10) = 180
(a) = a
2x – 10 + x + ten + x = 180
4x = 180
x = 180/4
x = 45

Question 4.
Reason Jamie solved the equation \(\frac{2}{3}\)ten + 4 = 2 + \(\frac{i}{two}\)x. Is his solution correct? Explicate.

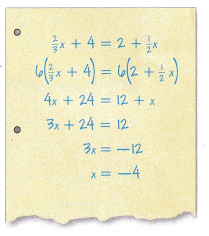
Answer:
The above-given solution:
two/iii x + 4 = ii + one/2 x
Simplification:
subtract '4' from both sides
2/3 x + 4 – 4 = 2 + one/two 10 – 4
ii/three x = 1/2 ten – two
subtract 1/2 x from both sides
2/3 x – 1/2 x = 1/2 x  – 2 + i/ii x
1/6 ten = -2
multiply both sides by 6
6 . 1/half dozen x = -two . half-dozen
x = -12
hence, Jamie is wrong.

Question v.
Karinne hit 4 more home runs than half the number of abode runs Lu hitting. Together they hit 10 dwelling house runs. Permit x represent the number of home runs Lu striking.
A. Write an equation to represent the state of affairs.
______________
Answer:
The equation is:
four + 1/2x = 10
B. Solve for ten.
______________
Respond:
1/2x = 10 – 4
1/2x = 6
x = 12

C. How many home runs did Lu hit?
______________
Reply:
iv + 1/2x= 10 (original equation)
Lu hits 12 home runs.
D. How many home runs did Karinne hit?
______________
Answer:
E. How tin you check your answer?
______________
______________
______________
______________

Question 6.
Construct Arguments Max and Corey solve the same equation but they apply different methods. Which method would you utilize? Explicate your answer.

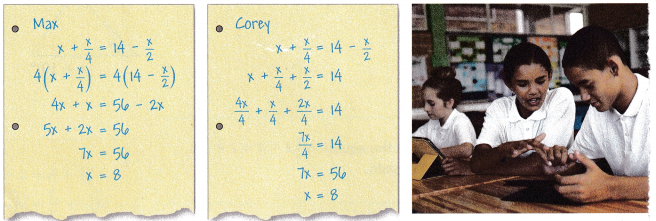
Answer:
I would choose Corey's answer.
Taking all similar terms into one side is easy to summate.
What Corey did was he grouped all like terms into one side and added all terms.
and then he used the LCM method to complete the simplification.

Question 7.
What is a showtime step to solve the equation 0.3n – 15 = 0.2n – 5?
______________
Reply:
The above-given equation:
0.3n – xv = 0.2n – 5
Multiply both sides by 10.
0.3n * x – 15 * 10 = 0.2n * 10 – 5 * 10
3n – 150 = 2n – 50
3n – 2n = -50 + 150
n = 100

Solve each equation. Check your solution.

Question 8.
3(x – 2) + six = v(x + 4)
______________
Answer:
The in a higher place-given equation:
3(x – 2) + 6 = 5(x + 4)
Simplification:
apply the distributive belongings.
3x – 6 + 6 = 5x + 20
3x = 5x + 20
subtract 5x from both sides
3x – 5x = 5x + xx – 5x
-2x = twenty
x = -x

Question 9.
2.2(4p + ii) = thirteen.ii
______________
Answer:
The in a higher place-given equation:
2.2(4p + 2) = 13.2
simplification:
multiply both sides by 10
ii.2(4p + 2) * ten = 13.2 * 10
22(4p + 2) = 132
divide both sides by 22
22(4p + ii)/22 = 132/22
4p + 2 = 6
4p = half dozen – two
4p = 4
p = 1

Question 11.
2(11t + 1.5t) = 12 – 5t
______________
Answer:
The above-given equation:
2(11t + i.5t) = 12 – 5t
Simplification:
add together like elements
two(12.5t) = 12 – 5t
25t = 12 – 5t
add together 5t to the both sides
25t + 5t = 12 – 5t + 5t
30t = 12
t = 12/30
t =2/5
t = 0.4

Question 12.
\(\frac{seven}{8}\)g – \(\frac{ane}{2}\) = \(\frac{3}{xvi}\)k + v
Reply:
The above-given equation:
7/8 k – 1/2 = 3/16m + 5
simplification:
become all like terms into one side
7/8 thou – 3/16 m = 5 + 1/2
7/8 m – 3/16 m = 10 + 1/2
vii/8 one thousand – iii/16 1000 = eleven/2
11/16 m = eleven/2
multiply both sides by 16
16 * eleven/sixteen m = 11/2 * 16
11m = 88
grand= 88/11
grand = viii

Question 13.
9(northward + 1) = 2(n – 1)
Respond:
The in a higher place-givene equation:
9(n + 1) = 2(northward – one)
simplification:
utilise the distributive holding
9n + 9 = 2n – 2
subtract 2n from both sides
9n + ix- 2n = 2n – 2 – 2n
7n + 9 = -2
7n = -2 – ix
7n = -xi
n = -xi/7

Question 14.
\(\frac{iv}{v}\)x – three = \(\frac{three}{10}\)10 + seven
Reply:
The above-given equation:
4/5 x – 3 = 3/x 10 + seven
add iii to the both sides
4/5 10 – 3 + 3 = iii/x x + 7 + 3
four/5 ten = 3/10 x + 10
subtract three/10 10 from both sides
4/five x – three/10 ten = 3/10 ten + 10 – 3/ten x
x(4/5 – 3/ten) = x
10(8 – 3/10) = x
x(5/ten) = 10
ten(1/2) = 10
1/2 x = 10
x = 20

Question fifteen.
-4(-5 – b) = \(\frac{1}{3}\)(b + 16)
Reply:
The in a higher place-given equation:
-4(-5 – b) = ane/3(b + xvi)
utilise distributive property
20 + 4b = i/3b + 16/3
subtract 20 from both sides
20 + 4b – 20 = one/3b + xvi/3 – twenty
4b = 1/3b + (16 – lx/3)
4b = i/3b – 44/3
decrease 1/3b from both sides
4b – i/3b = 1/3b – 44/iii – one/3b
b(four – 1/iii) = -44/3
b(12 – 1/3) = -44/3
b(xi/iii) = -44/3
11/3b = -44/3
b = -44/xi
b = -four

Question 16.
iii.6w = 2(0.8w + 12)
Answer:
The above-given equation:
3.6w = two(0.8w + 12)
apply distributive holding
3.6w = two * 0.8w + 12 * 2
3.6w = 1.6w + 24
3.6w – 1.6w = 24
2w = 24
w = 12

I'm in a Learning Mindset!

How is the outset stride in solving a multi-stride linear equation different from the outset step in solving a multi-step word problem?
Answer:
The principal goal in solving multi-stride equations, just like in one-step and two-footstep equations, is to isolate the unknown variable on ane side of the equation while keeping the constant or number on the opposite side.
– Become rid of whatsoever group symbols such as square brackets, parentheses, etc, by applying the Distributive Belongings of Multiplication over Addition.
– Simplify both sides of the equation, if possible, by combining like terms.
– Decide where you want to keep the variable because that will aid yous decide where to place the constant.
– Eliminate numbers or variables by applying opposite operations: addition and subtraction are opposite operations every bit in the case of multiplication and sectionalization.

Lesson 3.1 More Practise/Homework

Solve Multi-step Linear Equations

Question 1.
Elsie is planting a rectangular section of grass.

If the perimeter of the rectangle is 96 feet, what are the length and width of the rectangular department?
Reply:
The perimeter of the rectangle = two(a + b)
we know that,
the perimeter of the rectangle = 96
length = 6x – xv
width = x
96 = 2(6x – xv + x)
96 = two(5x – 15)
at present simplify the equation
96 = 10x – xxx
96 +30 = 10x
126 = 10x
switching sides
10x = 126
ten = 126/10
ten = 63/5
x = 12.six
Question ii.
Math on the Spot Solve each equation.
A. 3n + 1 = 19
__________
Respond:
The higher up-given equation:
3n + 1 = 19
3n = 19 – 1
3n = 18
n = eighteen/3
northward = 6

B. 21 = -2p – five
__________
Reply:
The above-given equation:
21 = -2p – 5
21 + 2p = -5
2p = -5 – 21
2p = -26
p = -26/2
p = -13

Question three.
Reason What step would you perform outset to solve the post-obit equation? Explain your reasoning.
\(\frac{one}{four}\)(12 – 8x) = \(\frac{ii}{3}\)(6x)
Reply:
The higher up-given equation:
1/4(12 – 8x) = two/3 (6x)
Multiply fractions: a(b/c) = a . b/c
1* (12 – 8x)/iv = 2/3 (6x)
12 – 8x/four = 4x
iii – 2x = 4x
three = 4x + 2x
3 = 6x
switching the sides
6x = 3
x = 1/two
x = 0.v

Question four.
Heather has a family phone plan. The monthly payment for the family plan includes a $70 charge for unlimited talk and text, a $20 line fee per phone, and a $22.91 equipment fee for each phone. Their total monthly bill is $241.64. Write and solve an equation to discover how many phones are on the program.
Answer:
The number of phones = f
The equation would exist:
f($70 + $xx + $22.91) = $241.64
f(112.91) = 241.64
f = 241.64/112.91
f = two.fourteen
approximately 2 phones.
Therefore, there are 2 phones are on the programme.

Solve each equation. Check your solution.

Question v.
a + 3(a – one) = iii(2 + i)
Answer:
The above-given equation:
a + 3(a – 1) = 3(2 + 1)
simplification:
a + 3a – 3 = three(iii)
a + 3a – 3 = ix
a + 3a = 9 + 3
4a = 12
a = 12/4
a = 3

Question half-dozen.
5y – 3(2 – y) = 10
Answer:
The above-given equation:
5y – three(2 – y) = 10
simplification:
5y – 6 + 3y = 10
8y – 6 = 10
8y = 10 + six
8y = 16
y = 16/viii
y = 2

Question seven.
one.2x – two = 7 + 0.9x
Respond:
The to a higher place-given equation:
1.2x – 2 = vii + 0.9x
multiply both sides by 10
1.2x * 10 – 2 * 10 = 7 * 10 + 0.9x * ten
12x – 20 = 70 + 9x
go all like terms into one side
12x – 9x = 70 + 20
3x = 90
ten = 90/3
x = 30

Question 8.
-k + 4(one thousand + i) = 2k
Answer:
The above-given equation:
-1000 + iv(k + 1) = 2k
simplification:
-k + 4k + 4 = 2k
3k + iv = 2k
get like terms on one side
3k – 2k = 4
k = 4

Question 9.
four(\(\frac{x}{6}\) + 5) = 2x + 10
Answer:
The above-givne equation:
4(x/6) + 5 = 2x + 10
4x/six + 5 = 2x + 10
get like on one side
2/3x – 2x = 10 -5
2x – 6x/3 = 5
-4x/three = v
-4x = 15
x = -fifteen/4

Question ten.
3w + \(\frac{w}{two}\) + 1 = 10 – westward
Answer:
The to a higher place-given equation:
3w + westward/2 + 1 = 10 – w
subtract 1 from both sides
3w + w/2 + 1 – 1 = 10 – w – 1
3w + west/2 = 9 – w
multiply both sides by two
3w * 2 + w/2 * 2 = 18 – w2
6w + west = eighteen – w2
7w = xviii – w2
add together w2 to both sides
7w + w2 = 18 – w2 + w2
9w = eighteen
w = 2

Test Prep

Question 11.
Which could be the showtime step in solving the equation 0.05x + 3 — 0.02x = iv?
A. Add 3 to each side of the equation.
B. Dissever each side of the equation by 100.
C. Multiply each side of the equation past 100.
D. Subtract 0.02x from each side of the equation.
Respond: Pick C is correct.
The above-given equation;
0.05x + 3 – 0.02x = four
0.03x + 3 = 4
Multiply both sides by 100
3x + 300 = 400
3x = 100
x = 33.333

Question 12.
Solve the equation. Check your solution.
\(\frac{three}{2}\)(ten + 6) = 16 + \(\frac{1}{two}\)(ten – 24)
x = ___
Answer:
The above-given equation:
three/2(x + 6) = 16 +1/ii(x – 24)
employ distributive holding
iii/2 10 + 3/2 * six = sixteen + 1/2 x – 1/2 * 24
iii/2 10 = one/2 x – 20
subtract 1/2 x from both sides
iii/two 10 – ane/ii ten = 1/ii x – 20 – 1/2 ten
x = -xx

Question 13.
Laurie earns $7.50 per hour at the fruit stand plus an extra $2.00 per 60 minutes on Sundays. One calendar week in August, she worked on Dominicus, Monday, and Wednesday. She worked the same number of hours on Monday and on Wednesday. On Dominicus she worked four hours. If she earned a full of $83.00 for the week, how many hours did Laurie work on Monday? Write and solve an equation.
Respond:
The equation would be:
we don't know the number of hours so assume it as 'h'
on Sundays, he works 4 hours and he gets $2 actress.
In a week, he works for three days
vii.50 + 2 = ix.50
In the question asked only for Monday hours
2(7.50h) + 9.50(4) = 83
14.50h + 38 = 83
fourteen.50h = 83 – 38
fourteen.50h = 45
h = 45/14.50
h = 3.1 (approximately three hours)

Question xiv.
Which equation has the solution x = 8?
A. 10 + 2x – four = \(\frac{1}{4}\)(3x + 4)
B. ten + \(\frac{1}{2}\)(ten + 8) = four(ane + three)
C. 2(10 – 4) = \(\frac{1}{4}\)(ane + 3) + x
D. x + iv(1 + 3) = \(\frac{ane}{two}\)(2x + 4)
Reply: Choice B is correct
solve all the equations
x + ane/2(x + eight) = 4(one +iii)
x + 1/2 10 + 1/2 . viii = 16
x + i/2 x + iv = 16
x + i/2 x = 16 – 4
ten(1 + 1/2) = 12
x(3/2) = 12
3x/2 = 12
3x = 24
x = eight

Question 15.
Each year Rolando saves 8% of his income. This twelvemonth he saved $3000; his salary was $2000 less than the previous year. What was his salary in the previous yr? Write and solve an equation.
Reply:
The previous income = N
The income he saves each year = eight% of N
In the present year, he saved = $3000
The salary = N – 2000
The equation would be:
8% (N – 2000) = 3000
eight/100(N – 2000) = 3000
N- 2000 = 3000 x 100/8
Northward – 2000 = 37500
Northward = 37500 + 2000
N = 39500.
Therefore, the previous salary is 39500.

Spiral Review

Question 16.
Triangle ABC is dilated by a calibration factor of 1.5 to course Triangle DEF. Are Triangles ABC and DEF coinciding? Why or why not?
Answer:
Congruent means when they are the aforementioned shape and same size. If triangle ABC is dilated to class triangle DEF, that ways that they will accept the same shape and the same size. So aye Triangles ABC and DEF will be coinciding to one another considering they will be the same shape, and they will take the same size as well.

Question 17.
A triangle has angles measuring 45°, 55°, and 80°. Information technology is dilated by a scale factor of ii. What are the bending measures of the dilated image?
Answer:
Dilations preserve bending measures, regardless of the scale gene. Therefore, the angle measures of the image will exist the same as that of the pre-image, so our reply is still 4545 °, 5555 °, and 8080 °.

3.1 Solving Quadratic Equations Answers,

Source: https://ccssmathanswers.com/into-math-grade-8-module-3-lesson-1-answer-key/

Posted by: ferrelltwoned.blogspot.com

Share this post